SENet: Squeeze-and Excitation Network

Introduction

Modern researches on CNN typically focus on enhancing the quality of spatial encodings. In this post, we discuss an architecture, called Squeeze-and-Excitation Network(SENet), that adaptively recalibrates channel-wise feature responses by explicitly modelling interdependencies between channels.

SENet

Motivation

SENet aims to capture channel-wise dependencies so that the network is able to increase its sensitivity to informative features which can be exploited by subsequent transformations. To do so, we introduce the squeeze and excitation operators. The squeeze operator summarizes the global information in each feature map, based on which, the excitation operation computes the corresponding weights.

SEBlock Architecture

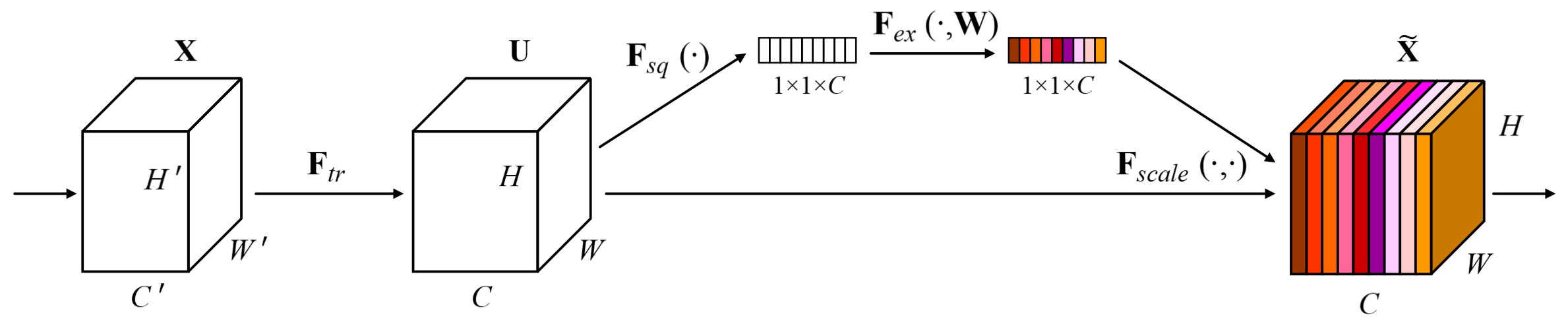
Figure.1. A Sequeeze-and-Excitation block

SENet consists a sequence of Squeeze-and-Excitation blocks depicted in Figure 1, which can be divided into four functions:

The transformation function \(\pmb F_{tr}\) could be any CNN layer/block, such as a residual block, that maps \(\pmb X\) to \(\pmb U\).
The squeeze function \(\pmb F_{sq}\) is a global average pooling layer which computes the mean of each channel plane. This results in a single vector for each \(\pmb U\).
The excitation operation \(\pmb F_{ex}\) is typically an MLP with sigmoid function as the output activation. It computes the desired weights of the corresponding channel planes in \(\pmb U\). We do not use softmax operation as we would like to allow multiple channels to be emphasised simultaneously. In practice, \(\pmb F_{ex}\) consists of two dense layers, where the first dense layer with ReLU as activation, serving as a dimensionality-reduction layer, maps the input vector \(\pmb z\) into a lower dimension vector. We can summarize \(\pmb F_{ex}\) as follows

\[\pmb s=\pmb F_{ex}(\pmb z)=\sigma(\pmb W_2ReLU(\pmb W_1\pmb z))\]

where \(\pmb W_1\in\mathbb R^{ {\over r}\times C}\), \(\pmb W_2\in\mathbb R^{ {\over r}\times C}\), \(\sigma\) and \(ReLU\) are sigmoid and relu activations. The reduction ratio \(r\) is recommended to be \(16\).

The rescale operation simply rescales channels of \(\pmb U\) using \(\pmb s\), which is done by a channel-wise multiplication between \(\pmb U\) by \(\pmb s\).

Ablation Study

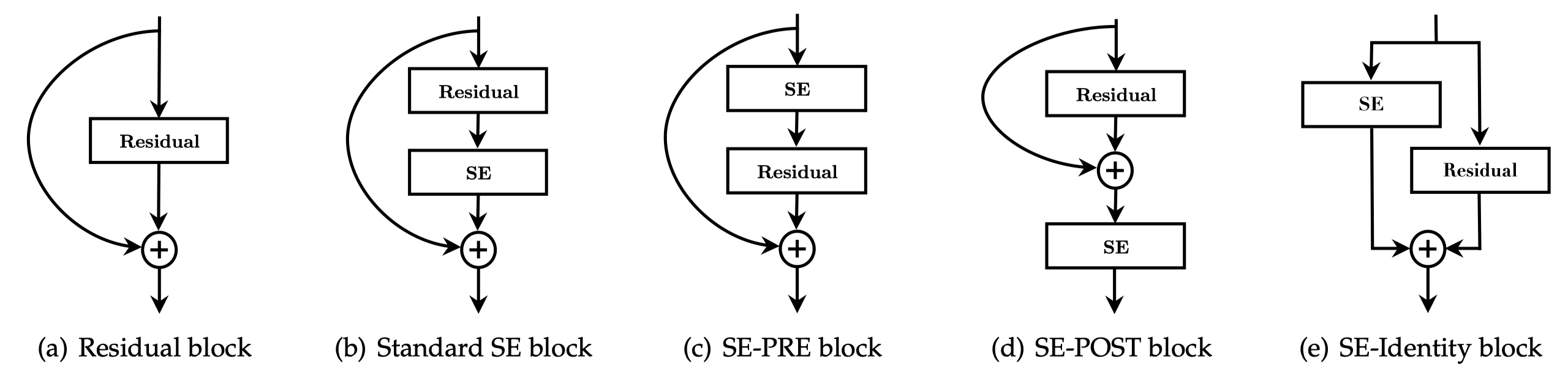
Figure 3. Different locations for the SE block in ResNet

Hu et al. conducts a series of ablation studies on components of the SE blocks. We summarize their results as follows:

Factors	Results
different \(r\) values \vert small \(r\) does not necessarily improve the performance. \(r=16\) achieves a good balance between accuracy and complexity.
max pooling layer as the squeeze operator	max pooling is effective, it performs slightly worse than average pooling on ImageNet dataset.
replace sigmoid activation with tanh and ReLU	both worsen the performance.
different locations for the SE block(See figure 3)	SE-PRE, SE-Identity and standard SE block performas similarly well, while SE-POST leads to a drop in performance.
place the SE block after \(3\times 3\) convolutional layer	it produces similar results with fewer parameters than the standard SE block.

References

Hu, Jie, Li Shen, Samuel Albanie, Gang Sun, and Enhua Wu. n.d. “Squeeze-and-Excitation Networks,” 1–13.